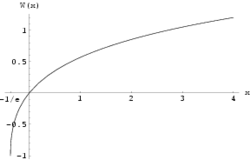
Graf av W 0 (x ) för -1/e ≤ x ≤ 4 Lamberts W-funktion är en matematisk funktion som används för att lösa ekvationer innehållande logaritmer eller exponentialfunktioner som inte kan elimineras algebraiskt. Den betecknas W och definieras som inversen till funktionen
f
(
w
)
=
w
e
w
{\displaystyle f(w)=we^{w}}
där w är ett komplext tal och e w Johann Heinrich Lambert .
Funktionen
f
(
w
)
=
w
e
w
{\displaystyle f(w)=we^{w}\,}
är inte injektiv på (−∞, 0) och W är därför en flervärd funktion på [−1/e , 0). För reella argument x ≥ −1/e kan man med kravet w ≥ −1 definiera en entydig funktion W 0 . Denna funktion uppfyller W 0 (0) = 0 och W 0 (−1/e ) = −1.
Lamberts W-funktion uppfyller
z
=
W
(
z
)
e
W
(
z
)
{\displaystyle z=W(z)e^{W(z)}\,}
och kan därför tillämpas genom att man skriver om ekvationer på formen
c
=
x
e
x
{\displaystyle c=xe^{x}}
c är konstant, varefter lösningen ges av
x
=
W
(
c
)
{\displaystyle x=W(c)}
t t lösas genom omskrivningen
2
t
=
5
t
⇒
{\displaystyle 2^{t}=5t\Rightarrow }
1
=
5
t
e
−
t
log
2
⇒
{\displaystyle 1=5te^{-t\log 2}\Rightarrow }
−
log
2
5
=
(
−
t
log
2
)
e
(
−
t
log
2
)
⇒
{\displaystyle {\frac {-\log 2}{5}}=(-t\log 2)\,e^{(-t\log 2)}\Rightarrow }
−
t
log
2
=
W
(
−
log
2
5
)
⇒
{\displaystyle -t\log 2=W\left({\frac {-\log 2}{5}}\right)\Rightarrow }
t
=
−
W
(
−
log
2
5
)
log
2
.
{\displaystyle t={\frac {-W\left({\frac {-\log 2}{5}}\right)}{\log 2}}.}
De ekvivalenta ekvationerna
x
=
log
x
{\displaystyle x=\log x}
x
=
e
x
{\displaystyle x=e^{x}}
x
=
−
W
(
−
1
)
≈
0
,
31813
−
1
,
33724
i
.
{\displaystyle x=-W(-1)\approx 0\mathrm {,} 31813-1\mathrm {,} 33724i.}
Ekvationen
x
x
=
z
{\displaystyle x^{x}=z}
x
=
log
z
W
(
log
z
)
=
exp
(
W
(
log
z
)
)
,
{\displaystyle x={\frac {\log z}{W(\log z)}}=\exp \left(W(\log z)\right),}
och det oändliga tornet av potenser
c
=
z
z
z
⋯
{\displaystyle c=z^{z^{z^{\cdots }}}\!}
antar vid konvergens värdet
c
=
W
(
−
log
z
)
−
log
z
.
{\displaystyle c={\frac {W(-\log z)}{-\log z}}.}
Några specifika värden är
W
(
−
π
/
2
)
=
i
π
/
2
{\displaystyle W\left(-\pi /2\right)=i\pi /2}
W
(
−
ln
a
a
)
=
−
ln
a
(
1
e
≤
a
≤
e
)
{\displaystyle W\left(-{\frac {\ln a}{a}}\right)=-\ln a\quad \left({\frac {1}{e}}\leq a\leq e\right)}
W
(
−
1
/
e
)
=
−
1
{\displaystyle W\left(-1/e\right)=-1}
W
(
−
log
2
/
2
)
=
−
log
2
{\displaystyle W\left(-\log 2/2\right)=-\log 2}
W
(
0
)
=
0
{\displaystyle W(0)=0\,}
W
(
e
)
=
1
{\displaystyle W(e)=1\,}
W
(
1
)
=
Ω
{\displaystyle W(1)=\Omega \,}
omegakonstanten )
W
(
−
1
)
≈
−
0.31813
−
1.33723
i
{\displaystyle W\left(-1\right)\approx -0.31813-1.33723{\rm {i}}\,}
W
′
(
0
)
=
1
{\displaystyle W'\left(0\right)=1\,}
Maclaurinserien till Lamberts W-funktion kan beräknas utifrån den implicita ekvationen
z
=
W
(
z
)
e
W
(
z
)
{\displaystyle z=W(z)e^{W(z)}\,}
genom Lagranges inverteringssats . Resultatet är
W
0
(
x
)
=
∑
n
=
1
∞
(
−
n
)
n
−
1
n
!
x
n
=
x
−
x
2
+
3
2
x
3
−
8
3
x
4
+
125
24
x
5
−
⋯
{\displaystyle W_{0}(x)=\sum _{n=1}^{\infty }{\frac {(-n)^{n-1}}{n!}}\ x^{n}=x-x^{2}+{\frac {3}{2}}x^{3}-{\frac {8}{3}}x^{4}+{\frac {125}{24}}x^{5}-\cdots }
som enligt kvottestet har konvergensradien 1/e .
Mer allmänt, för
r
∈
Z
,
{\displaystyle r\in \mathbb {Z} ,}
W
0
(
x
)
r
=
∑
n
=
r
∞
−
r
(
−
n
)
n
−
r
−
1
(
n
−
r
)
!
x
n
.
{\displaystyle W_{0}(x)^{r}=\sum _{n=r}^{\infty }{\frac {-r(-n)^{n-r-1}}{(n-r)!}}\ x^{n}.}
Derivatan ges av
d
d
x
W
(
x
)
=
W
(
x
)
x
(
1
+
W
(
x
)
)
{\displaystyle {\frac {d}{dx}}W(x)={\frac {W(x)}{x(1+W(x))}}}
Många uttryck innehållande Lamberts W-funktion kan integreras genom variabelsubstitutionen w = W (x ), det vill säga x = w ew
∫
W
(
x
)
d
x
=
x
(
W
(
x
)
−
1
+
1
W
(
x
)
)
+
C
.
{\displaystyle \int W(x)\,dx=x\left(W(x)-1+{\frac {1}{W(x)}}\right)+C.}
Lamberts W-funktion uppfyller differentialekvationen
z
(
1
+
W
)
d
W
d
z
=
W
z
≠
−
1
/
e
.
{\displaystyle z(1+W){\frac {dW}{dz}}=W\quad z\neq -1/e.}
∫
0
π
W
(
2
cot
2
(
x
)
)
sec
2
(
x
)
d
x
=
4
π
{\displaystyle \int _{0}^{\pi }W{\bigl (}2\cot ^{2}(x){\bigr )}\sec ^{2}(x)\;\mathrm {d} x=4{\sqrt {\pi }}}
∫
0
∞
W
(
1
x
2
)
d
x
=
2
π
{\displaystyle \int _{0}^{\infty }W\left({\frac {1}{x^{2}}}\right)\;\mathrm {d} x={\sqrt {2\pi }}}
∫
0
∞
W
(
x
)
x
x
d
x
=
2
2
π
{\displaystyle \int _{0}^{\infty }{\frac {W(x)}{x{\sqrt {x}}}}\mathrm {d} x=2{\sqrt {2\pi }}}
En approximation av
W
0
(
x
)
{\displaystyle W_{0}(x)}
x
{\displaystyle x}
W
0
(
x
)
=
ln
x
−
ln
ln
x
+
ln
ln
x
ln
x
+
O
(
(
ln
ln
x
ln
x
)
2
)
.
{\displaystyle W_{0}(x)=\ln x-\ln \ln x+{\frac {\ln \ln x}{\ln x}}+O\left(\left({\frac {\ln \ln x}{\ln x}}\right)^{2}\right).}
Speciella funktioner Gamma- och relaterade funktioner Zeta- och L -funktioner Besselfunktioner och relaterade funktioner Elliptiska funktioner och thetafunktioner Hypergeometriska funktioner Ortogonala polynom Andra funktioner
 Wikimedia Commons har media som rör Lamberts W-funktion.
Wikimedia Commons har media som rör Lamberts W-funktion.





































